ВАЛЕРИЙ
Глава 2. ‘’Критический анализ положений о “противоречиях”, будто бы «существующих» в математике
— ‘’О ЗЛОКАЧЕСТВЕННОЙ “ОСНОВЕ ” ЛЖЕНАУЧНОЙ ДЕЯТЕЛЬНОСТИ —
— III.3.5.4. ‘’Исследование мутации общества —
— III.3.5. ‘’Грессика —
— III.3. ‘’Обществика —
— Раздел III. Научные исследования —
— ‘’Объединенные исследования —
— ‘’Руководство по развитию российского общества —
S2335r41-2
Глава 2. ‘’Критический анализ положений
о “противоречиях”, будто бы «существующих»
в математике
2.1. ‘’Прямое и кривое
‘’Третье положение:
“
И все же дифференциальное исчисление, вопреки всем протестам здравого человеческого рассудка, приравнивает при известных условиях прямое и кривое друг к другу и достигает этим таких успехов, каких никогда не достигнуть здравому человеческому рассудку, упорствующему в своем утверждении, что тождество прямого и кривого является бессмыслицей.”
[1, 119]
“Мы уже упоминали, что одной из главных основ высшей математики является противоречие, заключающееся в том, что при известных условиях прямое и кривое должны представлять собой одно и то же.”
[1, 120]
Итак, в данном ‘’положении содержится принципиальное ‘’утверждение: “одной из главных основ высшей математики является противоречие”. Это принципиальное ‘’утверждение сделано на ‘’основании исходного ‘’утверждения о том, будто “дифференциальное исчисление ... приравнивает при известных условиях прямое и кривое друг к другу”.
Проверим оба эти ‘’утверждения.
Упоминаемые Ф. Энгельсом “известные условия” могут быть реально воспроизведены на любом конкретном ‘примере из дифференциального ‘исчисления. А именно, можно рассмотреть такие ‘’задачи, как ‘’Задача о касательной
[13, 242]
или ‘’Задача о скорости прямолинейного движения [там же, 244].
Однако, в известных ‘’задачах дифференциального ‘исчисления “прямое и кривое” не приравниваются ни при каких “известных условиях”. В частности, тригонометрическая ‘интерпретация математического ‘отношения ‘дифференциала ‘функции к ‘дифференциалу ‘аргумента представляет собой ‘тангенс ‘угла ‘наклона ‘касательной (являющейся прямой ‘линией), проведенной через любую наперед заданную ‘точку ‘графика дифференцируемой ‘функции (в типичных ‘задачах этот ‘график является кривой ‘линией) — как видно, в этом ‘случае “прямое” не приравнивается к “кривому”. (Более подробно это будет рассмотрено в четвертой ‘’главе настоящей ‘’работы.)
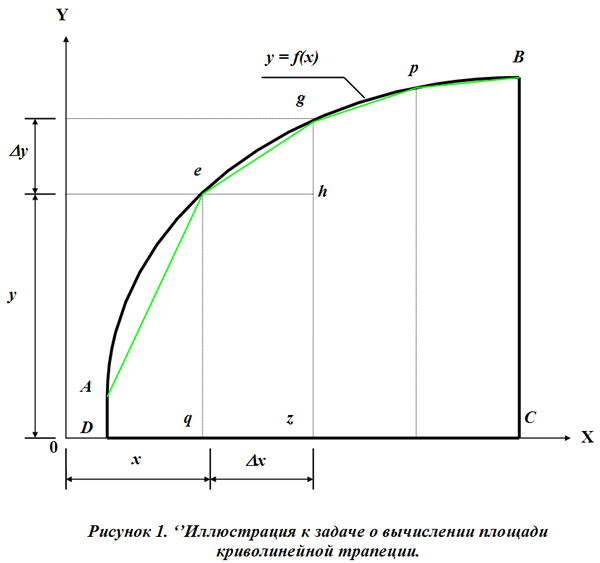
Можно предположить, что во второй ‘половине XIX-го ‘’века ‘’словосочетанием {дифференциальное исчисление} упоминали, в том числе, и интегральное ‘исчисление. В таком случае, Ф. Энгельс мог подразумевать хорошо известную ‘’задачу о ‘вычислении ‘площади криволинейной ‘трапеции. Эта ‘’задача состоит в ‘вычислении ‘площади S ‘фигуры (см. ‘’Рисунок 1), имеющей ‘форму криволинейной прямоугольной ‘трапеции, которая ограничена с одной ‘стороны кривой ‘линией AB, представляющей собой ‘график ‘функции y = f(x), а с другой ‘стороны ‘осью ‘координат 0X, при этом, ‘основаниями ‘трапеции являются два ‘перпендикуляра DA и CB, восстановленные от ‘оси 0X из граничных ‘точек D и C.
‘Применение интегрального и дифференциального ‘исчисления для ‘решения данной ‘задачи состоит в ‘’следующем.
Искомая ‘площадь S ‘фигуры ABCD делится на ‘части ‘перпендикулярами, восстановленными от ‘оси 0X через произвольно заданные ‘промежутки Dx. Если ближайшие ‘точки ‘пересечения каждого из ‘перпендикуляров с ‘кривой AB соединить между собой, как, в частности, соединены ‘точки e и g, то полученная таким ‘’путем ломаная ‘линия AegpB, состоящая из многих прямолинейных ‘отрезков, будет приблизительно повторять кривую ‘линию AB.
Из ‘’рисунка видно, что ‘площадь каждой из элементарных прямолинейных ‘трапеций (таких как qegz), почти совпадает с ‘площадью соответствующей ‘части криволинейной ‘трапеции, при этом ‘разница ‘площадей каждой элементарной прямолинейной ‘трапеции с соответствующей ‘частью криволинейной ‘трапеции будет тем меньше, чем на большее ‘количество ‘частей будет разделена ‘фигура ABCD.
Искомая ‘площадь S ‘фигуры ABCD, у которой AB есть кривая ‘линия, представляется как ‘предел, к которому «стремится» ‘сумма ‘площадей всех элементарных прямолинейных прямоугольных ‘трапеций, вписанных в ‘фигуру ABCD, при том ‘условии, что Dx «стремится» к ‘нулю. Очень важно обратить внимание на то, что ‘величина Dx ‘нулем не может быть, так как по ‘условиям ‘задачи ‘сумма всех ‘отрезков Dx должна представлять собой ‘отрезок DC.
Для достижения ‘целей, на которые направлен настоящий критический ‘’анализ, нет необходимости воспроизводить ‘’здесь весь ‘процесс математического ‘вычисления упомянутого ‘предела (производить интегральное и дифференциальное ‘исчисление), так как в этом ‘процессе нет никакого ‘упоминания и даже намека о том, что “прямое и кривое должны представлять собой одно и то же”.
Можно предположить, что Ф. Энгельс усмотрел “тождество прямого и кривого” в том, что ‘исчисление ‘площади S ‘фигуры ABCD, у которой ‘сторона AB ограничена кривой ‘линией y=f(x), практически осуществляется ‘путем ‘вычисления ‘предела к которому «стремится» ‘площадь ‘фигуры ABCD, ограниченной ломаной ‘линией (например, AegpB, состоящей из прямых ‘отрезков Ae, eg, gp, pB), при ‘условии, что Dx «стремится» к ‘нулю, но ‘нулем не является, т.е. при ‘условии, что ‘количество ‘изломов ‘линии AB будет «стремится» к бесконечно большому ‘числу.
Действительно, если попытаться изобразить графически такую ‘ситуацию, когда криволинейная прямоугольная ‘трапеция ABCD, разбита на большое ‘количество элементарных прямолинейных прямоугольных ‘трапеций, то появится визуальный эффект «совпадения» кривой ‘линии AB и вписанной в нее ломаной ‘линии, имеющей те же самые начальную и конечную ‘точки.
Но, этот визуальный эффект не может служить ‘основанием для ‘утверждения о том, будто “прямое и кривое должны представлять собой одно и то же”. При желании, вычерчивая ‘графики в более крупном ‘масштабе и более тонкими ‘линиями, можно убедиться, что, фактически, кривая ‘линия не совпадает с ломаной ‘линией, а кажущийся эффект их слияния обусловлен ограниченными техническими ‘возможностями чертить тончайшие ‘линии, а также и ‘способностями человеческого ‘глаза различать ‘линии при их близком ‘расположении. И тем более, умозрительное представление о «слиянии» кривой ‘линии и вписанной в нее ломаной ‘линии, состоящей из прямолинейных ‘отрезков, не может быть основанием для ‘утверждения о том, будто “прямое и кривое должны представлять собой одно и то же”.
Непреходящая практическая ‘ценность дифференциального и интегрального ‘исчисления состоит именно в том, что ‘математики разработали такие вычислительные ‘методы, пользуясь которыми можно производить ‘вычисление ‘предела, к которому «стремится» ‘сумма элементарных ‘площадей прямоугольных ‘трапеций, при том ‘условии, что, как бы ни была мала ‘величина Dx (т.е. на какое бы большое ‘количество элементарных ‘фигур не была разделена исходная ‘фигура), в этих ‘расчетах не делается ‘отождествление ломаной ‘линии, состоящей из прямых ‘отрезков, с кривой ‘линией.
Обратим внимание на то, что ‘результаты интегрального и дифференциального ‘исчисления строго ‘соответствуют ‘параметрам мирозданных ‘объектов. Абсолютная ‘точность конечного ‘результата математических ‘вычислений, соответствующая ‘оригиналу, достигается ‘путем точного ‘вычисления конкретной ‘величины математического ‘предела, к которому «стремится» промежуточный ‘результат ‘расчета приблизительной ‘модели (‘суммы ‘площадей ‘фигур, ограниченных прямыми ‘отрезками, составляющими ломаную ‘линию), при предполагаемом ‘условии теоретически бесконечного ‘уточнения этого промежуточного ‘результата.
Кстати, упомянутая приблизительная ‘модель может представлять собой ‘сумму ‘площадей ‘прямоугольников, (как это описано в ‘’учебнике
[13, 469]
), а не ‘трапеций, но ‘результат ‘исчисления — ‘предел, к которому «стремится» ‘сумма элементарных ‘площадей, получается тот же самый. Этот ‘’факт может служить не только яркой ‘демонстрацией объективного ‘характера ‘результатов интегрального и дифференциального ‘исчисления, но и еще одним ‘доказательством в пользу того, что в таком ‘исчислении не предусмотрено теоретически, и не происходит фактически ‘приравнивания “прямого и кривого”.
И еще. Если обратить внимание на то, что в дифференциальном и интегральном ‘исчислении Dx (или dx) не может быть ‘нулем (это есть главное исходное ‘условие ‘исчисления), то становится понятно, что, при любых сколь угодно малых ‘значениях Dx, ломаная ‘линия, которой аппроксимируют ‘график ‘функции, всегда остается составленной из многих прямых ‘отрезков.
Рассуждая методом от противного, тоже понятно, что “прямое и кривое” могли бы, гипотетически, “представлять собой одно и то же” только при одном ‘условии — когда ‘величина Dx была бы равна ‘нулю. Но это невозможно потому, что (как видно из ‘’рисунка и ясно из теоретического ‘анализа) ‘площадь приблизительной ‘модели, используемой для ‘расчета ‘предела, геометрически превратилась бы в ‘сумму, состоящую из нулей, из ничего — ‘«решение» превратилось бы в абсурдное «действие» над абсурдными мысленными представлениями. (Ф. Энгельс, как видно, не смог освоить математический ‘анализ, не понимал его и, в частности, никогда практически не применял дифференциальное и интегральное ‘исчисление.)
На ‘’основании ‘’анализа выше процитированного третьего ‘’положения можно констатировать, что, вопреки ‘’утверждениям Ф. Энгельса, в интегральном и дифференциальном ‘исчислении “кривое и прямое” не “приравниваются друг к другу”. Или, излагая то же самое, но другими ‘словами, ни при каких “известных условиях прямое и кривое” не “должны представлять собой одно и то же”.
Следовательно, ‘’утверждение Ф. Энгельса о том, будто “одной из главных основ высшей математики является противоречие”, - это лженаучная ‘’дезинформация.
2.2. ‘’О линиях
‘’Четвертое положение:
“
Но в высшей математике находит свое осуществление и другое противоречие, состоящее в том, что линии, пересекающиеся на наших глазах, тем не менее уже в пяти-шести сантиметрах от точки своего пересечения должны считаться параллельными, т.е. такими линиями, которые не могут пересечься даже при бесконечном их продолжении. И тем не менее высшая математика этими и еще гораздо более резкими противоречиями достигает не только правильных, но и совершенно недостижимых для низшей математики результатов.”
[1, 120]
В данном ‘’положении написано о пересекающихся и параллельных ‘линиях. Пересекающимися принято упоминать такие теоретически бесконечные ‘линии, которые имеют хотя бы одну общую ‘точку, при этом: пересекающиеся ‘линии могут быть как прямыми, так и кривыми; как лежащими в одной и той же ‘плоскости, так и расположенными в трехмерном ‘пространстве без особых ‘условий. Письменно изложенное ‘понятие о параллельных ‘линиях соответствует реальным ‘прототипам (описываемым мирозданным ‘объектам) только в том ‘случае, если рассматриваемые ‘линии лежат в одной и той же ‘плоскости и если эти ‘линии, будучи бесконечными ‘прямыми (т.е. не ограниченными по ‘длине), не имеют ни одной общей ‘точки.
Принимая во внимание эти известные с давних времен базовые математические ‘понятия, ‘утверждение Ф. Энгельса о том, будто “линии, пересекающиеся на наших глазах, тем не менее ... должны считаться параллельными”, можно воспринимать только как недоразумение. Ф. Энгельс выразил в этом ‘’фрагменте ‘’текста нечто такое, о чем он, может быть, прочитал в какой-нибудь фантастической ‘литературе, но, к сожалению, “забыл” сообщить своим ‘читателям об этом ‘источнике.
Отметим, что “в высшей математике находят свое осуществление” только такие ‘положения, которые соответствуют “низшей математике”, и дополняют последнюю в тех ‘случаях, когда математический ‘аппарат, предназначенный для обработки ‘величин, связанных неизменными ‘зависимостями (элементарными ‘функциями), оказывается недостаточным для обработки ‘величин, представляющих собой непрерывно меняющиеся ‘зависимости (‘функции ‘функций). (Будем надеяться, что геометрические ‘определения, свойственные исключительно евклидовой ‘геометрии, Ф. Энгельс не спутал с ‘определениями, свойственными ‘моделям искривленного ‘пространства или с ‘геометрией, разработанной для искривленной ‘поверхности.)
Так как в ‘’Четвертом положении отсутствуют ‘сведения, необходимые для его ‘анализа и ‘проверки, (в этом можно винить только самого Ф. Энгельса), то данное ‘’положение принципиально не может рассматриваться как математическое. Ведь ‘факт ‘применения в ‘рассуждениях ‘словосочетаний, применяемых математиками, таких как {пересекающиеся линии}, {параллельные линии}, {высшая математика} и др., при игнорировании соответствующих понятийных ‘описаний, выработанных ‘учеными-естествоиспытателями, не может служить ‘показателем того, что эти ‘рассуждения принадлежат к ‘математике: такие ‘’словосочетания может воспроизвести, например, и ‘попугай.
2.3. ‘’Математический корень
‘’Пятое положение:
“
Но уже и низшая математика кишит противоречиями. Так, например, противоречием является то, что корень из А должен быть степенью А, и тем не менее
Упомянутое “противоречие” можно понять двояко.
В одном ‘’варианте, можно предположить, что в данном ‘’положении Ф. Энгельс представил в качестве ‘’сторон упомянутого им “противоречия” два ‘’выражения: одно — словесное ‘’выражение “корень из А должен быть степенью А”; другое — алгебраическое ‘’выражение “
Однако, возможен и другой ‘’вариант «расшифровки» ‘’текста ‘’Пятого положения, а именно: “противоречием является то, что корень из А должен быть степенью А”. ‘’Здесь: одной стороной “противоречия” может быть понят “корень из А”; а другой стороной “противоречия” может быть понята “степень А”. В таком ‘’случае, далее следующее алгебраическое ‘’выражение может расцениваться как ‘’иллюстрация или как ‘’пояснение одной из ‘’сторон “противоречия”.
Отметим: если принять первый ‘’вариант, то в ‘ходе критического ‘’анализа будет исследован и второй ‘’вариант — как одна из ‘’сторон “противоречия”. Далее мы будем анализировать ‘’Пятое положение, рассматривая его по первому ‘’варианту.
Чтобы убедиться в том, что упомянутые ‘’выражения являются “противоречием”, присущим “низшей математике”, необходимо оба их записать в одной и той же ‘форме, например, в ‘’алгебраической. ‘Изложение ‘’выражений в одной ‘форме ‘записи необходимо для того, чтобы можно было, сопоставляя эти ‘’выражения, выявить и общие для них обоих математические ‘основания, и те присущие каждому их них ‘различия, которые должны быть противоречивыми.
Итак, мы преобразовываем ‘’выражение “корень из А должен быть степенью А” из словесной ‘’формы в ‘’алгебраическую. При этом, необходимо опираться на следующие общепринятые в математике ‘’определения.
‘’Первое определение: n-я ‘степень ‘числа B (алгебраически записывается как
A = Bn = B х B x B … B,
‘’где:
В ‘математике, при ‘формулировании математических ‘выражений в словесной ‘форме, допускается не упоминать ‘показатель ‘степени n, если n = 2. С ‘учетом данного ‘’упрощения, для частного ‘случая с ‘возведением в ‘квадрат, данное ‘’определение принимает ‘’вид: ‘степень ‘числа B (алгебраически обозначается как
‘’где:
‘’Второе определение: ‘Корнем n-й ‘степени из ‘числа A (алгебраически записывается как
или, то же самое —
если
В ‘математике допускается не записывать и не упоминать ‘степень ‘корня n, если n = 2 . C учетом такого ‘’упрощения, для конкретного ‘случая с квадратным ‘корнем, данное ‘’определение принимает следующий упрощенный ‘’вид: ‘корнем из A (алгебраически обозначается как
или, то же самое —
если
Если опираться на вышеизложенные общепринятые в ‘математике ‘определения, то становится понятно, что словесное ‘’выражение Ф. Энгельса “корень из А должен быть степенью А” является ошибочным. Действительно, в алгебраической ‘’форме это ‘’выражение должно иметь следующий ‘’вид (указывая подразумевающийся ‘показатель ‘степени, равный ‘’числу 2):
‘’где:
‘’Здесь видно, что словесное ‘’выражение, записанное в алгебраической ‘’форме, если его идентифицировать на ‘’основе общепринятых ‘’определений, не является математическим, так как соответствующее ему алгебраическое ‘’выражение, имеющее внешний ‘вид ‘равенства, не верно (математически абсурдно). Ведь при любых ‘значениях A правая ‘’часть этого ‘’выражения не может быть равна левой ‘’части (не “должна быть” левой ‘’частью).
Итак, если исходить из общепринятых математических ‘’определений, словесное ‘’выражение “корень из А должен быть степенью А” доджно быть признано ошибочным. Это ‘’выражение противоречиво по отношению к известным математическим ‘понятиям.
Следовательно, фактическая ‘’ситуация состоит в том, что Ф. Энгельс выдумал словесное ‘’выражение, являющееся ‘’противоречием по отношению к известным математическим ‘’определениям, а представил эту ‘’ситуацию так, будто “математика кишит противоречиями”.
Можно предположить, что в то ‘’время, когда Ф. Энгельс писал ‘’Анти-Дюринг, математические ‘’понятия могли быть не так четко отработаны, как это есть ‘’сегодня. Поэтому, мы попытаемся интерпретировать упомянутое выше словесное ‘’выражение Ф. Энгельса “корень из А должен быть степенью А” с учетом данного ‘’предположения.
Первая и средняя ‘’части словесного ‘’выражения не должны были пониматься иначе, чем их понимают ‘’сегодня. Что же касается последней ‘’части ‘’выражения, а именно ‘’записи “степенью A”, то можно предположить лишь еще один гипотетический ‘’вариант ее понимания — как ‘показателя ‘степени, в которую возводится ‘число A. Но даже и в этом ‘’случае словесное ‘’выражение “корень из А должен быть степенью А” в целом остается математически ошибочным, произвольным.
Наконец, если попытаться понять, что означает исследуемое словесное ‘’выражение на конкретном практическом ‘’примере, то получается следующий ‘’результат. Пусть A = 9. Тогда словесное ‘’выражение “корень из А должен быть степенью А” примет ‘’вид “корень из числа 9 должен быть степенью числа 9”, или, вычисляя ‘’корень, “число +3 (или число –3) должно быть степенью числа 9”. Как видно, здравый смысл (в том числе, и математическая ‘закономерность) здесь отсутствует. Других ‘вариантов понимания словесного ‘’выражения “корень из А должен быть степенью А” мы не можем представить.
Во всех рассмотренных ‘’вариантах словесное ‘’выражение “корень из А должен быть степенью А” невозможно понять так, чтобы оно соответствовало “низшей математике”. Следовательно, это ‘’выражение не может быть ‘стороной такого “противоречия”, которыми, будто бы “низшая математика кишит”.
Что же касается алгебраического ‘’выражения
Итак, общий ‘’вывод, который можно сделать по ‘’результатам ‘’анализа ‘’Пятого положения, состоит в том, что данное ‘’положение Ф. Энгельса не имеет никаких ‘оснований в ‘математике, а есть ‘’результат произвольного мышления Ф. Энгельса, содержащий в себе математическую ‘’ошибку. (Мы не исключаем возможности ошибочного ‘перевода, но, судя по ‘количеству обнаруживаемых ‘ошибок, вероятность ошибочного ‘перевода, практически, сводится к ‘нулю.)
2.4. ‘’Комплексные числа
‘’Шестое положение:
“
Противоречием является также и то, что отрицательная величина должна быть квадратом некоторой величины, ибо каждая отрицательная величина, помноженная сама на себя, дает положительный квадрат.”
[1, 120-121]
В данном ‘’положении Ф. Энгельс представил очередное свое “противоречие” следующими ‘’словами: “отрицательная величина должна быть квадратом некоторой величины”. В ‘’пределах ‘’анализа ‘’Шестого положения, мы будем упоминать этот ‘’текст как {‘’Формулировка “противоречия”}.
Вторая ‘’часть ‘’Шестого положения (после ‘’слова “ибо”) представляет собой ‘’пояснение, которым сопровождается ‘’Формулировка “противоречия”. (Обратим внимание на то, что эта ‘’часть ‘’положения не может рассматриваться как вторая ‘сторона “противоречия”, - это будет ясно из дальнейшего ‘’анализа).
Если рассматривать непосредственно ‘’Формулировку “противоречия”, то в ней самой невозможно усмотреть никакого дословно понимаемого ‘противоречия (в ней нет противоположных, или взаимоисключающих ‘изречений) — напротив, она представляет собой однозначное ‘’определение. По этому ‘’определению, любая “отрицательная величина” должна определяться как ‘результат математического ‘действия, конкретно, “быть квадратом некоторой (другой) величины”.
Но это ‘’определение сомнительное.
‘Математики сначала определяют с какими ‘величинами они имеют ‘дело, и только после этого, применительно к заранее определенному ‘ряду ‘величин (или ‘полю, или ‘кругу, или ‘области ‘чисел), они разрабатывают ‘правила ‘оперирования этими ‘величинами.
Например, если ‘математик имеет ‘дело с ‘рядом натуральных ‘чисел (1, 2, 3, 4, 5,...), то именно для ‘чисел этого ‘’ряда, он разрабатывает ‘правила ‘сложения, ‘вычитания, ‘умножения, ‘деления, ‘возведения в ‘степень; при этом, все ‘результаты математических ‘операций должны находиться в упомянутом ‘’ряду, т.е. представлять собой натуральные ‘числа.
Обратим внимание на то, что в ‘пределах ‘’ряда натуральных ‘чисел принципиально невозможно выполнить такие, например, ‘’операции, как {7 – 9}, или {1 – 2}, или {1 : 3}, или {5: 4}, так как ‘’результаты этих ‘’операций не являются натуральными ‘числами.
Из ‘’примера видно, что, в ‘пределах ‘’ряда натуральных ‘чисел, ‘’утверждение о том, будто “отрицательная величина должна быть квадратом некоторой величины”, - это абсурдное ‘’утверждение. Более того, для указанного ‘’ряда натуральных ‘чисел любое ‘упоминание об отрицательных ‘величинах — абсурдно.
Итак, мы можем констатировать, что в ‘пределах натурального ‘’ряда ‘чисел ‘’утверждение {“отрицательная величина должна быть квадратом некоторой величины”} не имеет никакого отношения к элементарной ‘математике, (‘предмет которой ограничен ‘’рядом натуральных ‘чисел).
Можно предположить, что Ф. Энгельс, записывая ‘’Шестое положение, имел в виду ‘’ряд всех рациональных ‘чисел, куда входят, кроме натуральных ‘чисел, еще и отрицательные ‘числа, ‘’число ‘’ноль и ‘числа ‘вида
Итак, в ‘пределах ‘’ряда рациональных ‘чисел ‘’Формулировка “противоречия” представляет собой ни что иное, как произвольное ‘’утверждение, которое не является ни исходным ‘принципом ‘математики, ни ‘следствием математических ‘действий. В упомянутых ‘пределах это ‘’утверждение также абсурдно.
Можно сделать еще одно ‘’предположение. Допустим, что Ф. Энгельс подразумевал условное ‘’множество так называемых «комплексных чисел», представляемых в общем ‘’виде как
Но, при этом, надо иметь в виду, что, рассматривая «комплексные числа», положительные и отрицательные ‘величины определяются совершенно по другому, в сравнении с рациональными ‘величинами. Так, например, утверждать о положительном или отрицательном ‘значениях «комплексного числа» 5-4i вообще не имеет смысла. Иногда условно считают, что, например, «комплексное число» -5-0i отрицательное, но такая ‘условность не имеет объективного ‘основания — ведь при этом любое «число» должно оставаться в условной области «комплекстных чисел», т.е. в области подразумеваемого. И только одно ‘число в условном множестве «комплексных чисел» действительно имеет отрицательное ‘’значение — это –1, которая входит в базовое ‘’определение «мнимого числа» i, и, следовательно, лежит в ‘’основе формирования представления о любом «комплексном числе».
С учетом выше сказанного, анализируемая ‘’Формулировка “противоречия” Ф. Энгельса о том, будто “отрицательная величина должна быть квадратом некоторой величины”, если и могла бы иметь отношение к ‘математике, то только в узкой ‘области ‘анализа известных ‘представлений о мнимых «комплексных числах» и только в том ‘’случае, если упомянутая Ф. Энгельсом “отрицательная величина” представляет собой именно ту –1, которая входит в базовое ‘’определение «мнимого числа» i.
Подставляя это единственно возможное безусловное (для «комплексных чисел») ‘’значение в ‘’Формулировку “противоречия”, получается следующее ‘’утверждение: “–1 должна быть квадратом некоторой величины”. Но, ведь это и есть ‘’формулировка базовой ‘’предпосылки, которая положена в ‘’основу ‘’создания известных ‘описаний «комплексных чисел». В таком ‘’случае, т.е. применительно к известным ‘описаниям «комплексных чисел», эта ‘’формулировка принципиально не может представлять собой “противоречие”, — напротив, в этой ‘’области она представляет собой однозначное ‘определение.
Принимая во внимание вышеизложенные ‘’сведения о натуральных и рациональных ‘числах, а также и о так называемых «комплексных числах», становится понятно, что первая ‘’часть анализируемого ‘’Шестого положения, (а именно: “Противоречием является также и то, что отрицательная величина должна быть квадратом некоторой величины”) относится, исключительно, к ‘’теме «комплексных чисел».
А теперь, внимание! В таком ‘’случае ‘’пояснение, которое изложено в ‘’Шестом положении за этой ‘’формулировкой, после ‘’слова “ибо”, должно тоже относится, исключительно, к ‘области «комплексных чисел».
Для удобства, выпишем вторую ‘’часть ‘’Шестого положения еще раз:
Как видно, эта ‘’формулировка не имеет никакого отношения к ‘области «комплексных чисел». (Вот почему вторая ‘’часть ‘’Шестого положения не может представлять собой ни одну из ‘’сторон “противоречия”, упомянутого Ф. Энгельсом.)
Итак, Ф. Энгельс в первой ‘’части ‘’Шестого положения упомянул ‘’отрывок из ‘описания «комплексных чисел», а во второй ‘’части этого же ‘’положения написал ‘’“подтверждение”, которое не относится к «комплексным числам». Понятно, что Ф. Энгельс не понимал того, о чем он писал. Он «слышал звон, да не знал откуда он»/!
Теперь должно быть понятно и то, что ни в одном из известных ‘’разделов ‘математики, которые могли бы иметь хоть какое-нибудь отношение к ‘’Формулировке “противоречия”, эта ‘’формулировка не может быть “противоречием”. Такого “противоречия” нет в ‘математике. Это “противоречие” вымышлено Ф. Энгельсом, как и то, будто такими “противоречиями” “математика кишит”.
В ‘’результате ‘’анализа ‘’Шестого положения можно сделать обоснованный ‘’вывод: ‘’утверждение “Противоречием является также и то, что отрицательная величина должна быть квадратом некоторой величины...” не соответствует фундаментальным ‘основам ‘математики. Кроме того, судя по этому ‘’утверждению, можно отметить еще одну конкретную ‘’ошибку Ф. Энгельса, еще один ‘’случай его непоследовательного мышления, еще один ‘’случай непонимания им ‘основ математической ‘науки, и, наконец, еще одну ‘’попытку представить “противоречие” будто бы существующим там, где его нет и быть не может.
‘’Приложение к шестому положению:
‘’Выше мы упоминали о том, что ‘’выражение
Однако, уяснив ‘основы ‘математики, становится понятно, что ‘’словосочетания “абсурдное противоречие” и “действительная бессмыслица”, не имеют никакого отношения к известным математическим ‘определениям, но являются подходящими ‘характеристиками для всех тех ‘’фрагментов ‘’книги Ф. Энгельса, которые мы уже проанализировали.
2.5. ‘’О “математике постоянных величин”
‘’Дополнение к третьему, пятому и шестому положениям:
“
Сама математика, занимаясь переменными величинами, вступает в диалектическую область, и характерно, что именно диалектический философ, Декарт, внес в нее этот прогресс. Как математика переменных величин относится к математике постоянных величин, так вообще диалектическое мышление относится к метафизическому.”
[1, 121]
Судя по данному ‘’тексту, Ф. Энгельс различал две “математики”: “математику постоянных величин” и “математику переменных величин”.
Выясним, что могут означать эти ‘’словосочетания в практическом ‘применении?
В известной ‘математике ‘величина называется постоянной, если она в математическом ‘решении ‘задач определенного ‘типа имеет неизменное количественное ‘значение в ‘виде ‘числа. ‘’Примером постоянной ‘величины может быть ‘’число p = 3,14..., которое применяется, в частности, в математическом ‘решении ‘задач ‘типа ‘определения ‘длины ‘окружности, проведенной на ‘плоскости, по известному ее ‘диаметру.
Обратим внимание на то, что ‘решение ‘задач данного ‘типа осуществляется на ‘основе математического ‘метода (т.е. оказывается применимым для любых ‘окружностей, проведенных на ‘плоскости) только в тех ‘случаях, если ‘величина ‘диаметра и ‘величина ‘длины ‘окружности считаются в этом ‘решении переменными ‘величинами (т.е. в разных ‘задачах данного ‘’типа они могут иметь ‘разные конкретные числовые ‘значения).
Уже в самом ‘’определении ‘’числа p, как универсальной ‘’константы, характеризующей известное ‘’отношение, свойственное любым ‘окружностям на ‘плоскости, содержится ‘’положение о том, что, от ‘задачи к ‘задаче, ‘диаметр и соответствующая ‘длина ‘окружности являются переменными ‘величинами.
Используя этот ‘’пример, можно попытаться представить себе “математику постоянных величин”. В такой “математике”, если иметь в виду тот же ‘’тип ‘задач, ‘решение каждой из ‘задач должно было бы основываться на исходной ‘’предпосылке о том, что и ‘диаметр ‘окружности, и ‘длина ‘окружности должны быть постоянными ‘величинами, выраженными конкретными ‘числами. Это означало бы, практически, что в каждом ‘случае надо было бы иметь дело только с данной конкретной ‘окружностью, имеющей конкретный ‘диаметр и конкретную ‘длину. При таких исходных ‘’условиях, каждая ‘задача определения ‘длины ‘окружности по ее ‘диаметру могла бы решаться только как специфический уникальный ‘’случай, не связанный ни с какими другими ‘задачами (в том числе, и с ‘задачами того же ‘’типа).
Известен только один ‘’метод, соответствующий таким ‘’условиям, — ‘’метод ‘построения ‘окружности на ‘плоскости с последующим ‘замером ее ‘длины. Но такой ‘’метод ‘решения практических ‘задач нельзя признать математическим — это исключительно эмпирический ‘’метод, осуществляемый без ‘применения ‘математики.
Для лучшего понимания нашего ‘’вывода, мы приведем еще один ‘’пример.
‘Решение ‘задач, ‘’типа ‘сложения ‘значений двух ‘величин, для ‘вычисления их ‘суммы, может осуществляться на ‘основе математического ‘метода только при том ‘’условии, если в этих ‘задачах хотя бы одно из ‘слагаемых является переменной ‘величиной. Ведь известные математические ‘правила ‘суммирования изначально предназначены для ‘обработки любых ‘чисел. Говоря другими ‘’словами, в математическом ‘решении ‘задач данного ‘’типа, ‘слагаемым можно придавать ‘разные ‘значения, в ‘зависимости от конкретных ‘условий той или иной ‘задачи.
В противном ‘’случае, а именно, если бы в ‘решении ‘задач данного ‘’типа оба ‘слагаемых предполагались бы только как постоянные ‘величины (конкретные ‘числа), то не имело бы смысла разрабатывать универсальные ‘правила ‘сложения, пригодные для любых ‘чисел, так как каждая ‘задача должна была бы рассматриваться как специфический ‘случай — так наверное и было в доисторические ‘времена, до ‘создания элементарной ‘математики.
Вышерассмотренных ‘’примеров должно быть достаточно для того, чтобы убедиться в принципиальной ошибочности ‘деления “математики” на “математику постоянных величин” и “математику переменных величин”. “Математика постоянных величин” в принципе не может быть.
Из выше ‘’изложенного должно быть понятно, что ‘разделение “математики” на ‘части по ‘признаку ‘наличия в ней постоянных или переменных ‘величин, не приемлемо и для ‘переменных второго ‘порядка, т.е. для переменных ‘величин, являющихся ‘функцией от такого ‘аргумента, который может принимать любые наперед заданные ‘значения.
Наконец, так как “
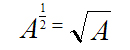 .”
[1, 120]
.”
[1, 120]
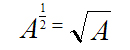 ”. Возможно, Ф. Энгельс полагал, что данное словесное ‘’выражение противоречит данному алгебраическому ‘’выражению.
”. Возможно, Ф. Энгельс полагал, что данное словесное ‘’выражение противоречит данному алгебраическому ‘’выражению.
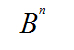 ) есть ‘произведение n ‘чисел, каждое из которых равно B. ‘Результат этого ‘произведения пусть будет A. В алгебраической ‘’форме данное ‘’определение записывается в следующем ‘’виде:
) есть ‘произведение n ‘чисел, каждое из которых равно B. ‘Результат этого ‘произведения пусть будет A. В алгебраической ‘’форме данное ‘’определение записывается в следующем ‘’виде:
‘число A упоминают как n-ю ‘степень ‘числа B;
‘число B упоминают как ‘основание ‘степени;
‘число n — ‘показатель ‘степени.
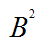 ) есть ‘произведение ‘числа B самого на себя. ‘Результат этого ‘произведения пусть будет A. В алгебраической ‘форме данное упрощенное ‘’определение имеет следующий ‘’вид:
) есть ‘произведение ‘числа B самого на себя. ‘Результат этого ‘произведения пусть будет A. В алгебраической ‘форме данное упрощенное ‘’определение имеет следующий ‘’вид:
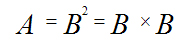 ,
,
‘число A упоминают как ‘степень ‘числа B;
‘число B упоминают как ‘основание ‘степени;
‘’число 2 — ‘показатель ‘степени.
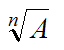 ) называется ‘число (пусть это будет B), n-я ‘степень которого равна A. В алгебраической ‘’форме данное ‘’определение имеет следующий ‘’вид:
) называется ‘число (пусть это будет B), n-я ‘степень которого равна A. В алгебраической ‘’форме данное ‘’определение имеет следующий ‘’вид:
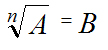 , при исходном ‘условии, что
, при исходном ‘условии, что 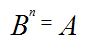 ;
;
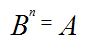 , то
, то 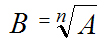 .
.
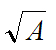 ) называется ‘число (обозначим его как B), ‘квадрат которого равен А. То есть, алгебраически:
) называется ‘число (обозначим его как B), ‘квадрат которого равен А. То есть, алгебраически:
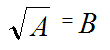 , при исходном ‘’условии, что
, при исходном ‘’условии, что 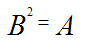 ;
;
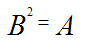 , то
, то 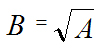 .
.
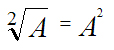 ,
,
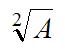 — соответствует первой ‘’части словесного ‘’выражения, а именно записи “корень из А”;
— соответствует первой ‘’части словесного ‘’выражения, а именно записи “корень из А”;
знак {=} — соответствует средней ‘’части словесного ‘’выражения, а именно ‘’записи “должен быть”;
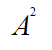 — соответствует последней ‘’части словесного ‘’выражения, а именно ‘’записи “степенью А”.
— соответствует последней ‘’части словесного ‘’выражения, а именно ‘’записи “степенью А”.
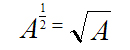 , упомянутого Ф. Энгельсом в ‘’Пятом положении (в качестве второй ‘’стороны “противоречия”), то оно представляет собой разные ‘варианты ‘записи одного и того же математического ‘’выражения, т.е. оно, само по себе, не содержит никакого “противоречия”.
, упомянутого Ф. Энгельсом в ‘’Пятом положении (в качестве второй ‘’стороны “противоречия”), то оно представляет собой разные ‘варианты ‘записи одного и того же математического ‘’выражения, т.е. оно, само по себе, не содержит никакого “противоречия”.
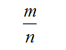 , ‘’где m и n — целые ‘числа и
, ‘’где m и n — целые ‘числа и 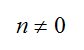 . Но и в ‘пределах ‘’ряда рациональных ‘чисел ‘’утверждение Ф. Энгельса о том, будто “отрицательная величина должна быть квадратом некоторой величины”, не выражает “противоречия”. Напротив, легко доказывается, что в ‘пределах ‘’ряда рациональных ‘чисел такое ‘’утверждение ошибочно: ведь какое бы из рациональных ‘чисел не было возведено в ‘квадрат, в ‘результате никогда не получится отрицательное рациональное ‘число (как частный ‘случай этого ‘’контрдовода, смотри ‘’пояснение, которое сопровождает ‘’Формулировку “противоречия” после ‘’слова “ибо”).
. Но и в ‘пределах ‘’ряда рациональных ‘чисел ‘’утверждение Ф. Энгельса о том, будто “отрицательная величина должна быть квадратом некоторой величины”, не выражает “противоречия”. Напротив, легко доказывается, что в ‘пределах ‘’ряда рациональных ‘чисел такое ‘’утверждение ошибочно: ведь какое бы из рациональных ‘чисел не было возведено в ‘квадрат, в ‘результате никогда не получится отрицательное рациональное ‘число (как частный ‘случай этого ‘’контрдовода, смотри ‘’пояснение, которое сопровождает ‘’Формулировку “противоречия” после ‘’слова “ибо”).
a + bi ,
‘’где:
a и b — произвольные действительные ‘числа;
i — так называемая «мнимая единица» — «мнимое число», ‘квадрат которого равен –1 (то есть 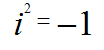 , или, что то же самое,
, или, что то же самое, 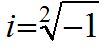 ).
).
“… ибо каждая отрицательная величина, помноженная сама на себя, дает положительный квадрат.”
“Поэтому квадратный корень из минус единицы есть не просто противоречие, а даже абсурдное противоречие, действительная бессмыслица. И все же
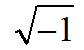 является во многих случаях необходимым результатом правильных математических операций; более того, что было бы с математикой, как низшей, так и высшей, если бы ей запрещено было оперировать с
является во многих случаях необходимым результатом правильных математических операций; более того, что было бы с математикой, как низшей, так и высшей, если бы ей запрещено было оперировать с 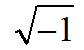 ?”
[1, 121]
?”
[1, 121]
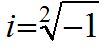 является однозначным (т.е. принципиально непротиворечивым) ‘’определением, созданным для формирования представлений о «комплексных числах». Мы упоминали и о том, что данное ‘’выражение, которое может быть представлено в ‘’виде
является однозначным (т.е. принципиально непротиворечивым) ‘’определением, созданным для формирования представлений о «комплексных числах». Мы упоминали и о том, что данное ‘’выражение, которое может быть представлено в ‘’виде 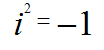 , фактически представлено Ф. Энгельсом как “отрицательная величина”, которая “должна быть квадратом некоторой величины”. Таким образом, по Ф. Энгельсу получается, будто это однозначное ‘’определение и есть “абсурдное противоречие, действительная бессмыслица”.
, фактически представлено Ф. Энгельсом как “отрицательная величина”, которая “должна быть квадратом некоторой величины”. Таким образом, по Ф. Энгельсу получается, будто это однозначное ‘’определение и есть “абсурдное противоречие, действительная бессмыслица”.